找出数组的第 K 大和

题目描述

给你一个整数数组 nums 和一个正整数 k 。你可以选择数组的任一子序列并且对其全部元素求和。

数组的第 k 大和定义为：可以获得的第 k 个最大子序列和（子序列和允许出现重复）

返回数组的第 k 大和。

子序列是一个可以由其他数组删除某些或不删除元素排生而来的数组，且派生过程不改变剩余元素的顺序。

注意：空子序列的和视作 0 。

来源：力扣（LeetCode）链接：https://leetcode.cn/problems/find-the-k-sum-of-an-array 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

示例 1：

输入：nums = [2,4,-2], k = 5 输出：2 解释：所有可能获得的子序列和列出如下，按递减顺序排列：

6、4、4、2、2、0、0、-2 数组的第 5 大和是 2 。

来源：力扣（LeetCode）链接：https://leetcode.cn/problems/find-the-k-sum-of-an-array 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

第k小子序列

首先考虑非负数组的情况下，然后求第k小的子序列的问题。

我们定义一个二元组(sum,i)，表示和为sum，结尾为i(第i位不算)的子序列。然后维护一个小根堆，每次取出堆顶，即sum最小的元素，然后将第i位的元素，考虑第i-1位元素选或者不选，将(sum+arr[i],i+1)和(sum+arr[i]-arr[i-1],i+1)添加到堆中，操作k次，第k次取出来的堆顶就是第k小的子序列。

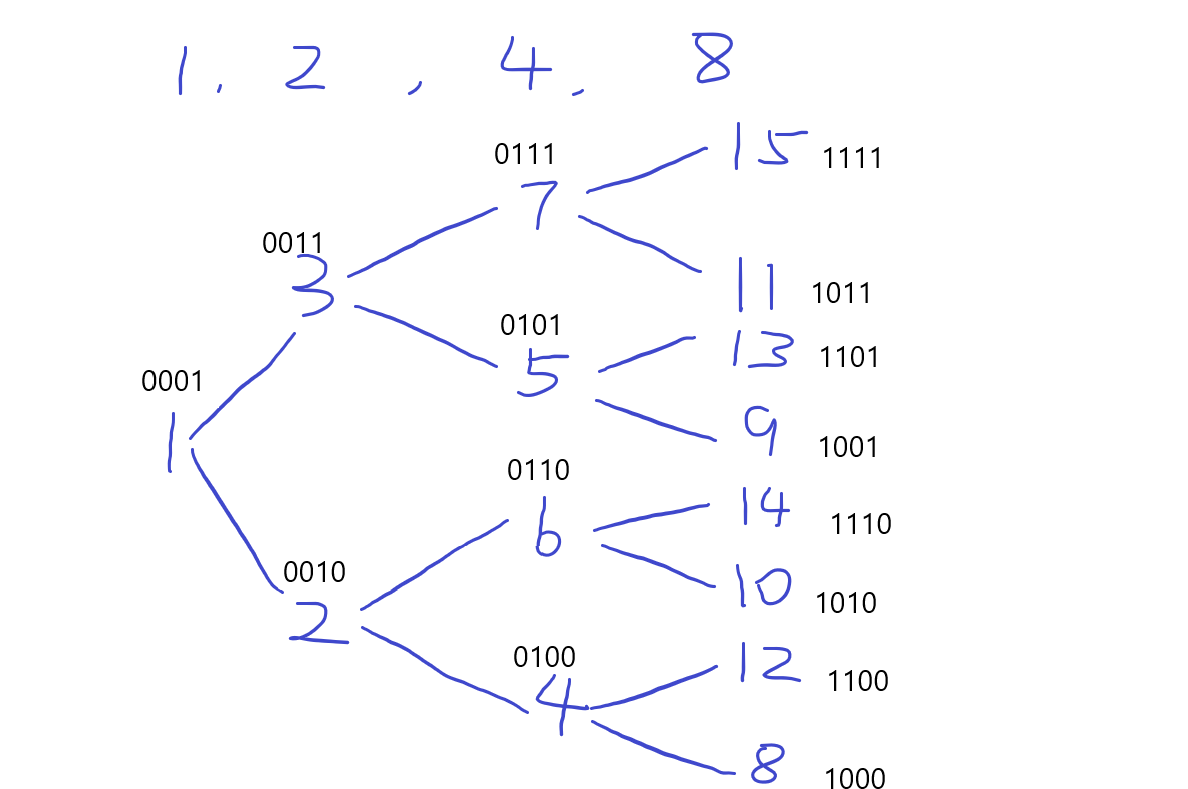
考虑如下序列【1,2,4,8】，我们知道他的子序列和范围为0~15

注意观察图例中的二进制表示，可以发现对于第i位，比如8，这一列产生的数字的二进制第4位都是1，表示这个数被选择，即对应sum+arr[i]。然后可以发现数字15和11是由7产生而来，而11=7+8-4，即表示第i-1个数我们不取，即对应sum+arr[i]-arr[i-1]。可以看到对于第i位数字，他产生的那列数字，对应的第i为都是1的，这是因为在其之前的数字，第i为都是0，即已经将低位全部考虑完全了。

进一步我们知道一个长度为n的数组，其子序列个数为2^n，也即对应了二进制的表示情况

第k小画图

考虑负数情况

上述我们已经知道如何求一个非负数组的第k小子序列了，那么我们回到本题，考虑负数的情况。

首先这题要求的是第k大子序列和，可以转化为【最大的子序列和-第k小的子序列和】

首先最大的子序列和sum，即为数组中所有非负元素的和。当需要求比最大子序列和更小的子序列和时，相当于从sum中减去一些正数或者加上一些负数，因此将负数取绝对值，统一转化成减去一些正数的做法，然后对正数的数组求第k小的子序列和。

求第k小子序列和

同理，如果这题要求的是第k小的子序列和，那么我们同样可以转化为【最小的子序列和+第k小的子序列和】，同样，当需要求比最小子序列和更大的子序列和时，相当于给sum加上一些正数或者减去一些负数，同样将负数取绝对值，统一转化成加上一些正数的做法。

code

typedef long long LL;
class Solution {
public:
    long long kSum(vector<int>& nums, int k) {
        priority_queue<pair<LL,int>,vector<pair<LL,int>>,greater<pair<LL,int>>> pq;
        LL sum=0;
        for(int i=0;i<nums.size();++i) {
            // 求最大子序列和
            if(nums[i]>0) sum+=nums[i];
            // 负数取绝对值
            nums[i]=abs(nums[i]);
        }
        // 数组排序，必要
        sort(nums.begin(),nums.end());
        // 求第k小子序列和
        pq.emplace(0,0);
        while(--k) {
            auto p=pq.top();
            pq.pop();
            LL val=p.first;
            int i=p.second;
            if(i<nums.size()) {
                pq.emplace(val+nums[i],i+1);
                if(i) pq.emplace(val-nums[i-1]+nums[i],i+1);
            }
        }
        auto p=pq.top();
        return sum-p.first;
    }
};