柱状图中最大的矩形(单调栈)

柱状图中最大的矩形

题目描述

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

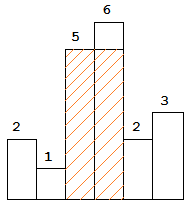
柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。

图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

来源：力扣（LeetCode）链接：https://leetcode-cn.com/problems/largest-rectangle-in-histogram 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

将题目抽象成对于一个高度h，对其向左右延伸，延伸时需要保证其他高度必须大于h，延伸后的长度就是该位置上的高度h所能形成的矩形的宽度。

例如对于第一个柱子高度为2，左延伸为0，右延伸为0，因为1<2，则其宽度为1，则该位形成的矩形面积为2。

注意这里不能降低高度去延伸，必须使用高度2去延伸。

因此，可以进一步将问题抽象成，对于一个数h，在数组中向左右分别找到第一个小于它的数，这之间的距离就是宽度。

因此考虑使用单调栈来解决。

https://oi-wiki.org/ds/monotonous-stack/

对于样例，[2,1,5,6,2,3]

维护一个单调增栈，向右找到第一个小于它的数，然后记录两个数之间的距离，即下标相减

初始栈空，2入栈，此时栈[2]
1尝试入栈，此时栈顶2>1，则2出栈，因为1入栈导致了2出栈，则表示1是第一个小于它的数，则记录下2的距离为2-1=1，此时栈[1]
5入栈，6入栈，此时栈[1,5,6]
2尝试入栈，6>2，6出栈，2是第一个小于6的数，记录6的距离为5-4=1
2尝试入栈，5>2，5出栈，2是第一个小于5的数，记录5的距离为5-3=2
2入栈，此时栈[1,2]
3入栈，此时栈[1,2,3]
对于还在栈内的元素，其距离都为数组长度6减去下标位置
最终向右延伸的长度数组为[1,5,2,1,2,1]

然后对该数组翻转，再用上述方法求一次，则是向左延伸的长度[1,2,1,1,3,1]

将两个数组求和，去掉重复的当前位置，则长度数组为[1,6,2,1,4,1]

再用长度数组和高度数组求乘积，得到面积数组[2,6,10,6,8,3]，该数组的最大值即为答案

code

type node struct {
	idx, val int
}

func largestRectangleArea(heights []int) int {
	h := make([]node, len(heights))
	reh := make([]node, len(heights))
	for k, v := range heights {
		h[k] = node{k, v}
		reh[len(reh)-k-1] = node{len(reh) - k - 1, v}
	}
	stack1 := make([]node, 0, len(heights))
	stack2 := make([]node, 0, len(heights))
	stack1 = append(stack1, h[0])
	stack2 = append(stack2, reh[0])

	left := make([]int, len(heights))
	right := make([]int, len(heights))
	for i := 0; i < len(heights); i++ {
		left[i], right[i] = len(heights), len(heights)
	}

	for i := 1; i < len(heights); i++ {
		if h[i].val > stack1[len(stack1)-1].val {
			stack1 = append(stack1, node{i, h[i].val})
			goto re
		}
		for len(stack1) >= 1 && stack1[len(stack1)-1].val > h[i].val {
			right[stack1[len(stack1)-1].idx] = i
			stack1 = stack1[:len(stack1)-1]
		}
		stack1 = append(stack1, node{i, h[i].val})
	re:
		if reh[i].val > stack2[len(stack2)-1].val {
			stack2 = append(stack2, node{i, reh[i].val})
			continue
		}
		for len(stack2) >= 1 && stack2[len(stack2)-1].val > reh[i].val {
			left[stack2[len(stack2)-1].idx] = i
			stack2 = stack2[:len(stack2)-1]
		}
		stack2 = append(stack2, node{i, reh[i].val})
	}
	ans, lens := -1, len(heights)
	for i := 0; i < len(heights); i++ {
		//right[i] - i
		//left[lens-i-1] - lens + i +1
		//-1
		ans = max(ans, heights[i]*(right[i]-i+left[lens-i-1]-lens+i))
	}
	return ans
}

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

单调栈的其他例题

下一个更大元素 I

给你两个没有重复元素的数组 nums1 和 nums2 ，其中nums1 是 nums2 的子集。

请你找出 nums1 中每个元素在 nums2 中的下一个比其大的值。

nums1 中数字 x 的下一个更大元素是指 x 在 nums2 中对应位置的右边的第一个比 x 大的元素。如果不存在，对应位置输出 -1 。

来源：力扣（LeetCode）链接：https://leetcode-cn.com/problems/next-greater-element-i 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

单调栈对nums2数组求一次即可

code

func nextGreaterElement(nums1 []int, nums2 []int) []int {
	hash := make(map[int]int)
	stack := make([]int, 0, len(nums2))
	stack = append(stack, nums2[0])
	for i := 1; i < len(nums2); i++ {
		if nums2[i] < stack[len(stack)-1] {
			stack = append(stack, nums2[i])
            continue
		}
		for len(stack) >= 1 && nums2[i] > stack[len(stack)-1] {
			hash[stack[len(stack)-1]] = nums2[i]
			stack = stack[:len(stack)-1]
		}
		stack = append(stack, nums2[i])
	}
	ans := make([]int, len(nums1))
	for i := 0; i < len(nums1); i++ {
		if v, ok := hash[nums1[i]]; ok {
			ans[i] = v
		} else {
			ans[i] = -1
		}
	}
	return ans
}

每日温度

请根据每日气温列表，重新生成一个列表。对应位置的输出为：要想观测到更高的气温，至少需要等待的天数。如果气温在这之后都不会升高，请在该位置用 0 来代替。

例如，给定一个列表 temperatures = [73, 74, 75, 71, 69, 72, 76, 73]，你的输出应该是 [1, 1, 4, 2, 1, 1, 0, 0]。

提示：气温列表长度的范围是 [1, 30000]。每个气温的值的均为华氏度，都是在 [30, 100] 范围内的整数。

来源：力扣（LeetCode）链接：https://leetcode-cn.com/problems/daily-temperatures 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

单调栈对温度列表求一次即可，在入栈出栈的时候记录下标位置用于算距离即可，与柱状图矩形类似

code

type node struct {
	idx, val int
}

func dailyTemperatures(T []int) []int {
	arr := make([]node, len(T))
	for k, v := range T {
		arr = append(arr, node{k, v})
	}
	stack := make([]node, 0, len(T))
	ans := make([]int, len(T))
	stack = append(stack, arr[0])
	for i := 1; i < len(arr); i++ {
		if arr[i].val < stack[len(stack)-1].val {
			stack = append(stack, arr[i])
			continue
		}
		for len(stack) >= 1 && arr[i].val > stack[len(stack)-1].val {
			ans[stack[len(stack)-1].idx] = arr[i].idx - stack[len(stack)-1].idx
			stack = stack[:len(stack)-1]
		}
		stack = append(stack, arr[i])
	}
	return ans
}

下一个更大元素 II

给定一个循环数组（最后一个元素的下一个元素是数组的第一个元素），输出每个元素的下一个更大元素。数字 x 的下一个更大的元素是按数组遍历顺序，这个数字之后的第一个比它更大的数，这意味着你应该循环地搜索它的下一个更大的数。如果不存在，则输出 -1。

输入: [1,2,1]
输出: [2,-1,2]
解释: 第一个 1 的下一个更大的数是 2；
数字 2 找不到下一个更大的数； 
第二个 1 的下一个最大的数需要循环搜索，结果也是 2。

来源：力扣（LeetCode）链接：https://leetcode-cn.com/problems/next-greater-element-ii 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路

对于环形数组，则将数组复制多一份即可[1,2,1]–>[1,2,1,1,2,1]

这样就能求到数h后面的和前面的数

这里在实际写的时候，可以不用复制一份，可以用取模的方法模拟复制，节省一份内存

code

type node struct {
	idx, val int
}

func nextGreaterElements(nums []int) []int {
    if len(nums) == 0 {
		return []int{}
	}
	stack := make([]node, 0, len(nums))
	ans := make([]int, len(nums))
	for k := range ans {
		ans[k] = -1
	}
	stack = append(stack, node{0, nums[0]})
	for i := 1; i < len(nums)*2; i++ {
		j := i % len(nums)
		if nums[j] < stack[len(stack)-1].val {
			stack = append(stack, node{j, nums[j]})
			continue
		}
		for len(stack) >=1 && nums[j] > stack[len(stack)-1].val {
			ans[stack[len(stack)-1].idx] = nums[j]
			stack = stack[:len(stack)-1]
		}
		stack = append(stack, node{j, nums[j]})
	}
	return ans
}