转变数组后最接近目标值的数组和
题目描述
给你一个整数数组 arr 和一个目标值 target ,请你返回一个整数 value ,使得将数组中所有大于 value 的值变成 value 后,数组的和最接近 target (最接近表示两者之差的绝对值最小)。
如果有多种使得和最接近 target 的方案,请你返回这些整数中的最小值。
请注意,答案不一定是 arr 中的数字。
来源:力扣(LeetCode) 链接:https://leetcode-cn.com/problems/sum-of-mutated-array-closest-to-target 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
枚举答案
对于每个value,按题目条件计算出其与target的差值。可以得到函数,x为value,f(x)为差值。
这个函数有三种可能的情况,单调递增,单调递减和先单调减后单调增,凸函数
这个函数的极限值的变量值就是答案
因此,对于凸函数求极值采用三分搜索
https://blog.csdn.net/wzy_1988/article/details/9075963
https://oi-wiki.org/basic/binary/#_9
对于三分搜索:
设左边界为l,右边界为r,左右边界中点为lm,中点和右边界的中点为rm
则存在以下情况
-
f(lm)<f(rm)
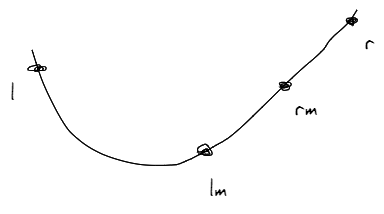
则极值点在靠近lm处,则缩小右边界,边界更新为[l,rm]
-
f(lm)>f(rm)
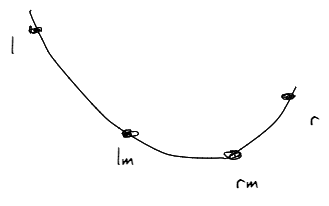
则极值点在靠近lm处,则缩小左边界,边界更新为[lm,r]
-
f(lm)==f(rm)
对于这种情况,按数字的定义,此时l==r,但在计算机的计算中,由于整数相除是不一定整除的.
因此出现f(lm)==f(rm),有以下几种情况
-
l==r
-
l==r-1
比如l=4,r=5,则计算出来的lm和rm都是4
-
l==r-2
比如l=3,r=5,则计算出来的lm和rm都是4
对于以上无论哪种情况,l和r的差值都在≤2。
因此只需要特殊处理以下,m和左右两个值那个更小,那个就是答案。
-
code
func check(arr, arrsum []int, val int) int {
// 使用二分+前缀和来求差值和
pos := sort.Search(len(arr), func(i int) bool {
return arr[i] > val
})
if pos == 0 {
return val * len(arr)
}
return arrsum[pos-1] + (len(arr)-pos)*val
}
func abs(a int) int {
if a < 0 {
return -a
}
return a
}
func findBestValue(arr []int, target int) int {
// 对原数组排序
sort.Ints(arr)
// 求前缀和
arrsum := make([]int, len(arr))
arrsum[0] = arr[0]
for i := 1; i < len(arr); i++ {
arrsum[i] = arrsum[i-1] + arr[i]
}
l, r := 0, arr[len(arr)-1]
var m, mm int
for l < r {
m = (r-l)/2 + l
mm = (r-m)/2 + m
// 特殊情况处理
if m == mm {
ls, ms, rs := abs(check(arr, arrsum, l)-target), abs(check(arr, arrsum, m)-target), abs(check(arr, arrsum, r)-target)
if ms < ls && ms < rs {
return m
}
if ms < ls {
return r
}
return l
}
if abs(check(arr, arrsum, m)-target) < abs(check(arr, arrsum, mm)-target) {
r = mm
} else {
l = m
}
}
return l
}